A Homogeneous System Is Always Consistent

Note that a homogeneous system Ax0 will always be consistent as it always has the solution x0 the trivial solution. Properties of a Homegeneous System 1A homogeneous system is ALWAYS consistent since the zero solution aka the trivial solution is always a solution to that system. Is homogeneous equation always consistent. To sketch the graph of pair of linear equations in two variables we draw two lines representing the equations. Alternately I think what you were looking for is the Rouche-Capelli theorem which basically states that a system of equations will be consistent if the rank of the augmented matrix equals the rank of A. The only two options for a homogeneous system of equations is either a unique solution trivial solution or infinitely many solutions. By Theorem HSC we know the system is consistent because the zero vector is always a solution of a homogeneous system.

Moreover the general solution contains n - r 4 - 3 1 arbitrary constant.

So ρ A ρ A O n. If rank of co-efficients matrix number of unknowns unique solution which is the trivial solution. Example AHSAC Archetype C as a homogeneous system. X y x y. Let x 3 a where a is arbitrary. Show activity on this post.

Solved A Linear Homogeneous System Of Equations Is Always Chegg Com

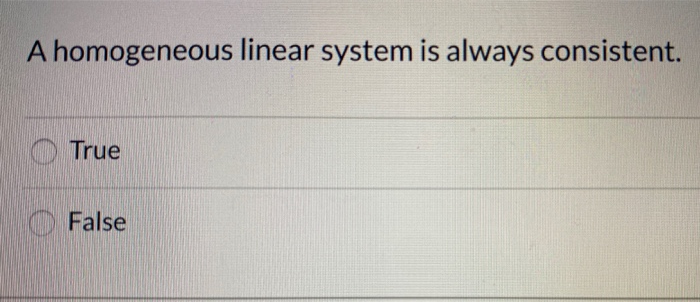
A homogeneous system is always consistent. Solution in parametric form to the system is the particular solution to the system. A linear homogeneous system of equations is always consistent The homogeneous equation Ax 0 has the trivial solution ifand only if the equation has at least one free variable. There is a special type of system which requires additional study.

From the last row of C K x 4 0. Dimension The dimension of a vector space is the number of vectors in. Homogenous systems are linear systems in the form Ax 0 where 0 is the 0 vector.

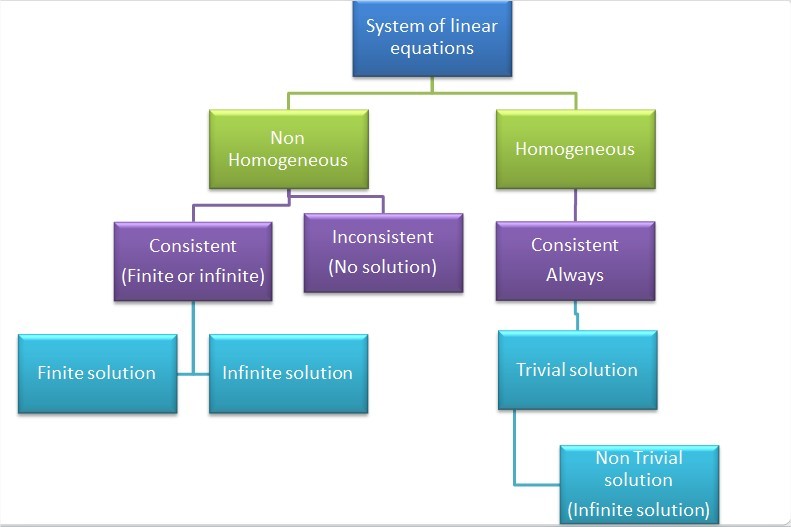
Since a homogeneous system is always consistent the solution set is nonempty. Solutions to the homogeneous system Auvecx zerovec can be considered as column vectors in Rntext so the solution set to this system is a subcollection of a vector space. Show activity on this post.

0 k where k 0 and is a separator within augmented matrix. Answered Jul 1 13 at 2151. Then x 1 10 11a and x 2 -2 - 4a.

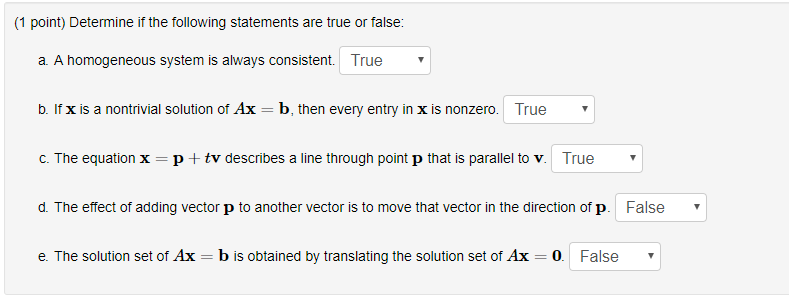
I If both the lines intersect at a point then there exists a unique solution to the pair of linear equations. True There is only one way to parametrically represent the solution set of a linear equation. A homogeneous system has the form.

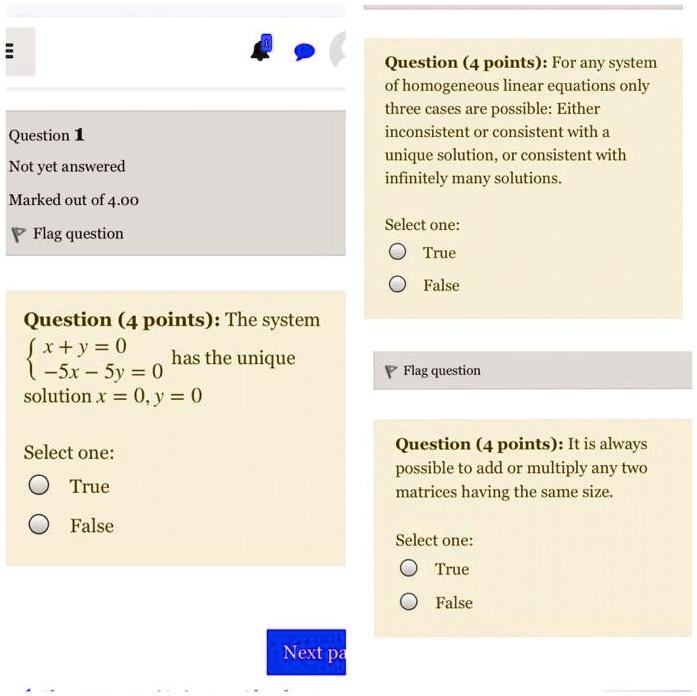
Thus a homogenous equation is always consistent. Note that a homogeneous system Ax0 will always be consistent as it always has the solution x0 the trivial solution. A system is defined as inconsistent if its row-reduced echelon form contains a row of form 0 0 0.

Since the rank r of the system and the number n of unknowns are equal the only possibility is. At the point left 00 right the equation is always consistent as this point is always the solution of the linear equation.

Homogeneous Systems Of Linear Equations Youtube

Professor Dr S K Bhattacharjee Department Of Statistics Ppt Video Online Download

Solved Mark Each Statement As True Or False Remember That A Chegg Com

Solved Mark Each Statement True Or False Justify Each Chegg Com

Solved A Homogeneous Linear System Is Always Consistent O Chegg Com

Solved 1 Point True False Problem Mark Each Statement As Chegg Com

Solved 1 Point Determine If The Following Statements Are Chegg Com

The Homogeneous System Ax 0

Consistency Of Homogeneous System Of Linear Equation Trivial And Non Trivial Solution Of Linear Youtube

Linear Algebra Example Problems Homogeneous System Of Equations Youtube

Solved Mark Each Statement True Or False Justify Each Chegg Com

Homogeneous System Of Linear Equation Is Consistent Quiz 1 Solutions Math 341 Docsity

Underdetermined Overdetermined System Of Linear Equations Consistent Inconsistent No Of Solutions Youtube

Linear Equations Gauss Cramer S Ppt Download

System Of Linear Equations Consistent Inconsistent And Number Of Solutions Youtube

Homogeneous Systems Of Algebraic Equations A Homogeneous Ho Mo Geen Ius System Of Linear Algebraic Equations Is One In Which Pdf Free Download

Solved Mark Each Statement True Or False Justify Each Chegg Com

5 Homogeneous Systems Pdf Free Download

Underdetermined And Overdetermined System Solutions For Homogeneous System Of Equations Youtube

Review On Linear Algebra Ppt Download

Which Of The Following Statements Is True None Gauthmath

25 Points State Whether Each Of The Following Statem Itprospt

Solved Any System Of N Equations In N Unknowns Has At Most N Solutions A Homogeneous System Of Linear Equations Is Always Consistent If U V W Course Hero

Homogeneous System

Answered Which Of The Following Statement Is Bartleby

Linear Algebra Textbook Reference Website Homework Submission J

Solved 2 If The Rank Of The Coefficient Matrix Of A System Of N Linear Equations In N Unknowns Equals The Rank Of The Augmented Matrix Then The System Has Unique Solution Always

Linear Algebra

Basic Terminology For Systems Of Equations In A Nutshell E L Lady 3x 1 7x 2 4x 3 0 5x 1 8x 2 12x 3 0 Pdf Free Download

Homogeneous And Nonhomogeneous Systems Of Linear Equations Youtube

Matrices Chapter 8 1 8 8 Ch 2 Contents 8 1 Matrix Algebra 8 1 Matrix Algebra 8 2 Systems Of Linear Algebra Equations 8 2 Systems Of Linear Ppt Download

Mat223 Final Exam Review Sheet Pdf Eigenvalues And Eigenvectors Matrix Mathematics

Lecture 2 Pdf System Of Linear Equations Matrix Mathematics

Solved True False Exercises 59 And 60 Determine Whether Each Statement Is True Or False If A Statement Is True Give Reuson Or Cite An Appropriate Statement From The Text Ir A Statement

Solved Which Of The Statements Below Is Not True With Chegg Com

Section 8 2 Solving A System Of Equations Using Matrices Guassian Elimination Pdf Free Download

Solved Complete The Following Statements A System A X B Is Homogeneous If Is A Solution If The Number Of Unknowns In A System Of Linear Equ Course Hero

Summary Possibilities For The Solution Set Of A System Of Linear Equations Problems In Mathematics

19 Let M N Be Two Positive Integers Which Of Th Itprospt

Wrean Ca

Class Note3 Lecture Notes 3 Math 1004 Calculus For Engineering Studocu

System Of Linear Equations Wikipedia

Solved Question 4 Points For Any System Of Homogeneous Linear Equations Only Three Cases Are Possible Either Inconsistent Or Consistent With A Unique Solution Consistent With Infinitely Many Solutions Question 1 Not Yet

Math 1104 1 5 Solution Set Of Linear Solutions Flashcards Quizlet

Solved A Homogeneous Linear System Is Always Consistent O Chegg Com

System Of Linear Equations Simultaneous Equations Brilliant Math Science Wiki

Chapter 1 Section 1 3 Consistent Systems Of Linear Equations Ppt Download

Rdscollege Ac In

Homogeneous System

Dimension The dimension of a vector space is the number of vectors in.

Is it a subspace. A linear homogeneous system of equations is always consistent The homogeneous equation Ax 0 has the trivial solution ifand only if the equation has at least one free variable. A system is defined as inconsistent if its row-reduced echelon form contains a row of form 0 0 0. We know that the general equation of a Homogeneous system of linear equations with two variables in it is ax by 0. I If both the lines intersect at a point then there exists a unique solution to the pair of linear equations. A homogeneous system has the form. Since your system equals 0 it is impossible to have k 0 rendering the system consistent. The solution of the system is given by x 1 10 11a x 2 -2 - 4a x 3 a x 4 0 or. Example AHSAC Archetype C as a homogeneous system.

Since the rank r of the system and the number n of unknowns are equal the only possibility is. We know that the general equation of a Homogeneous system of linear equations with two variables in it is ax by 0. A homogeneous system of eqs. Homogenous systems are linear systems in the form Ax 0 where 0 is the 0 vector. As you might have discovered by studying Example AHSAC setting each variable to zero will always be a solution of a homogeneous system. The equation x p tu describes a line through v parallel to p. A system of homogeneous equations of degree 0 is always consistent since setting all the variables to 0 provides a solution.